Question

14．已知函数$f（x）=aln（x-a）-\frac{1}{2}{x^2}+x$（a＜0）．
（Ⅰ）当a=-3时，求f（x）的单调递减区间；
（Ⅱ）若函数f（x）有且仅有一个零点，求实数a的取值范围．

Answer 1

分析 （Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的递减区间即可；
（Ⅱ）求出函数的导数，通过讨论a的范围，求出函数的单调区间，结合函数的图象求出a的具体范围即可．

解答 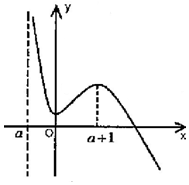解：（Ⅰ）∵a=-3，∴$f（x）=-3ln（x+3）-\frac{1}{2}{x^2}+x$，
故$f'（x）=\frac{-x（x+2）}{x+3}（x＞-3）$，
令f′（x）＜0，解得-3＜x＜-2或x＞0，
即所求的单调递减区间为（-3，-2）和（0，+∞）；
（Ⅱ）∵$f'（x）=\frac{a}{x-a}-x+1=\frac{-x[x-（a+1）]}{x-a}$（x＞a），
令f′（x）=0，得x=0或x=a+1，
（1）当a+1＞0，即-1＜a＜0时，
f（x）在（a，0）和（a+1，+∞）上为减函数，在（0，a+1）上为增函数，
由于f（0）=aln（-a）＞0，当x→a时，f（x）→+∞，
当x→+∞时，f（x）→-∞，于是可得函数f（x）图象的草图如图：
此时函数f（x）有且仅有一个零点．
即当-1＜a＜0对，f（x）有且仅有一个零点；
（2）当a=-1时，$f（x）=-ln（x+1）-\frac{1}{2}{x^2}+x$，
∵$f'（x）=\frac{{-{x^2}}}{x+1}≤0$，∴f（x）在（a，+∞）单调递减，
又当x→-1时，f（x）→+∞．当x→+∞时，f（x）→-∞，
故函数f（x）有且仅有一个零点；
（3）当a+1＜0即a＜-1时，
f（x）在（a，a+1）和（0，+∞）上为减函数，在（a+1，0）上为增函数，
又f（0）=aln（-a）＜0，当x→a时，f（x）→+∞，当x→+∞时，f（x）→-∞，
于是可得函数f（x）图象的草图如图：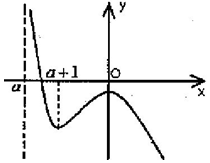

此时函数f（x）有且仅有一个零点；
综上所述，所求的范围是a＜0．

点评 本题考查了函数的单调性、最值问题，考查导数的应用以及分类讨论思想，转化思想，考查函数的零点问题，是一道综合题．