
���� �ٸ�����������η��ӱ���̬�ֲ�N��0����2�����õ���̬���߹��ڦ�=0�Գƣ�����P��-2���Ρ�2��=0.4���������P���Σ�2����
��ȷ������f��x��ͼ�����x=-1�Գƣ��ڣ�-1��+�ޣ��ϵ������������ɵó����ۣ�
����ֱ֪��l1��ax+3y-1=0��l2��x+by+1=0����l1��l2�ij�Ҫ������a+3b=0��
��� �⣺�١���������η�����̬�ֲ�N��0����2��������̬���߹��ڦ�=0�Գƣ�
��P��-2���Ρ�2��=0.4����P���Σ�2��=$\frac{1}{2}$��1-0.4��=0.3����ȷ��
�ڡߺ���f��x-1����ż��������f��-x-1��=f��x-1�����ຯ��f��x��ͼ�����x=-1�Գƣ��ߺ���f��x-1���ڣ�0��+�ޣ��ϵ����������ຯ��f��x���ڣ�-1��+�ޣ��ϵ���������
��f��log2$\frac{1}{8}$��=f��-3��=f��1������$\frac{1}{8}$��2��1��2${\;}^{\frac{1}{8}}$����f��2${\;}^{\frac{1}{8}}$����f��log2$\frac{1}{8}$����f[��$\frac{1}{8}$��2]����ȷ��
����ֱ֪��l1��ax+3y-1=0��l2��x+by+1=0����l1��l2�ij�Ҫ������a+3b=0���ʲ���ȷ��
�ʴ�Ϊ���٢ڣ�
���� ���⿼�����������жϣ�������̬�ֲ��������ĵ����ԣ�����ֱ�ߴ�ֱ�ij�Ҫ������֪ʶ�ۺ���ǿ��


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
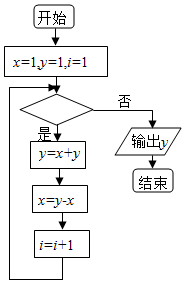 ִ����ͼ�ij����ͼ���������yֵΪ5�����жϿ��п�����������ǣ�������
ִ����ͼ�ij����ͼ���������yֵΪ5�����жϿ��п�����������ǣ�������| A�� | i��3 | B�� | i��4 | C�� | i��5 | D�� | i��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | C�� | ��Ҫ | D�� | �dz�ַDZ�Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com