练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
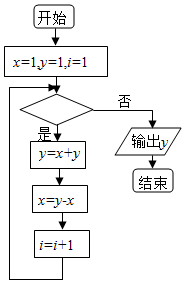
    13．执行如图的程序框图，若输出的y值为5，则判断框中可填入的条件是（　　）
    A．i＜3B．i＜4C．i＜5D．i＜6

    分析 根据程序框图，依次写出每次循环得到的运行结果，根据i=4时，退出循环，输出y的值为5，可得判断框内应填入的条件．

    解答 解：模拟执行程序，可得
    x=1，y=1，i=1
    满足条件，执行循环体，y=2，x=1，i=2
    满足条件，执行循环体，y=3，x=2，i=3
    满足条件，执行循环体，y=5，x=3，i=4
    由题意，此时应该不满足条件，退出循环，输出y的值为5．
    故判断框中可填入的条件是i≤3？或i＜4？．
    故选：B．

    点评 本题主要考查了程序框图的应用，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．已知幂函数y=（m-1）2•x${\;}^{{m^2}-4m+2}}$在（0，+∞）上单调递增，则m的值为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知长方体ABCD-A1B1C1D1中，AB=2，BC=BB1=$\sqrt{2}$，在四边形ABC1D1内随机取一点M，则满足∠AMB≥135°的概率为（　　）
    A．$\frac{π}{8}$B．$\frac{π-2}{8}$C．$\frac{2π-3\sqrt{3}}{12}$D．$\frac{2\sqrt{2}-2}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若[x]表示不超过x的最大整数，执行如图所示的程序框图，则输出S的值为（　　）
    A．3B．5C．7D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．给出下列命题：
    ①已知ξ服从正态分布N（0，δ2），且P（-2≤ξ≤2）=0.4，则P（ξ＞2）=0.3；
    ②函数f（x-1）是偶函数，且在（0，+∞）上单调递增，则f（2${\;}^{\frac{1}{8}}$）＞f（log2$\frac{1}{8}$）＞f[（$\frac{1}{8}$）2]
    ③已知直线l1：ax+3y-1=0，l2：x+by+1=0，则l1⊥l2的充要条件是$\frac{a}{b}$=-3，
    其中正确命题的序号是①②（把你认为正确的序号都填上）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，以点F2为圆心的圆与双曲线的渐近线相切，切点为P．若∠F1PF2=$\frac{2π}{3}$，则双曲线的离心率为（　　）
    A．$\frac{{\sqrt{13}}}{3}$B．$\frac{{\sqrt{21}}}{3}$C．$\sqrt{5}$D．$\sqrt{37}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，过点F作x轴的垂线交两渐近线于点A，B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+u$\overrightarrow{OB}$（λ，μ∈R），λ2+u2=$\frac{5}{8}$，则双曲线的离心率为（　　）
    A．$\frac{{2\sqrt{3}}}{3}$B．$\frac{{3\sqrt{5}}}{5}$C．$\frac{{3\sqrt{2}}}{2}$D．$\frac{9}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．求下列情况下的概率．
    （1）在集合{-3，-2，-1，1，2，3}中随机取两个数，分别记为a，b，求使得方程x2+2ax-b2+π=0有实根的概率
    （2）在区间[-π，π]内随机取两个数，分别记为a，b，求使得方程x2+2ax-b2+π=0有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在直二面角α-l-β中，线段AB的端点A，B分别在α，β内，且AB与α，β所成的角均为30°，则AB与l所成的角为（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    同步练习册答案