
| 日销售量(本) | 小于100 | [100,200) | 大于等于200 |
| 奖励金额(元) | 0 | 100 | 200 |

分析 (1)设A1表示事件“日销售量小于100个”,A2表示事件“日销售量在[100,200)个”,A3表示事件“日销售量大于等于200个”,B表示事件“在未来连续3天里,店员共获得奖励200元”.由此利用相互独立事件概率乘法公式,能求出在未来连续3天里,店员共获得奖励200元的概率.
(2)由已知得X的可能取值为0,100,200,300,400,500,600,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答 解:(1)设A1表示事件“日销售量小于100个”,
A2表示事件“日销售量在[100,200)个”,A3表示事件“日销售量大于等于200个”,
B表示事件“在未来连续3天里,店员共获得奖励200元”.
P(A1)=(0.003+0.005)×50=0.4,
P(A2)=(0.006+0.004)×50=0.5,
P(A3)=0.002×50=0.1,
P(B)=0.4×0.52×3+0.42×0.1×3=0.348.
(2)由已知得X的可能取值为0,100,200,300,400,500,600,
P(X=0)=0.43=0.064,
P(X=100)=0.42×0.5×3=0.24,
P(X=200)=0.4×0.52×3+0.42×0.1×3=0.348,
P(X=300)=0.4×0.5×0.1×6+0.53=0.245,
P(X=400)=0.4×0.12×3+0.52×0.1×3=0.087,
P(X=500)=0.5×0.12×3=0.015,
P(X=600)=0.13=0.001,
∴随机变量X的分布列为:
| X | 0 | 100 | 200 | 300 | 400 | 500 | 600 |
| P | 0.064 | 0.24 | 0.348 | 0.245 | 0.087 | 0.015 | 0.001 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
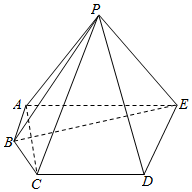 在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE
在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com