
分析 化简去根号f(x)=$(x\sqrt{x\sqrt{x}})^{\frac{1}{2}}$=${x}^{\frac{1}{2}}$•${x}^{\frac{1}{4}}$•${x}^{\frac{1}{8}}$=${x}^{\frac{7}{8}}$,从而求导.
解答 解:f(x)=$\sqrt{x\sqrt{x\sqrt{x}}}$
=$(x\sqrt{x\sqrt{x}})^{\frac{1}{2}}$
=${x}^{\frac{1}{2}}$$(x\sqrt{x})^{\frac{1}{4}}$
=${x}^{\frac{1}{2}}$•${x}^{\frac{1}{4}}$•${x}^{\frac{1}{8}}$=${x}^{\frac{7}{8}}$,
故f′(x)=$\frac{7}{8}$•${x}^{-\frac{1}{8}}$,
故答案为:$\frac{7}{8}$•${x}^{-\frac{1}{8}}$.
点评 本题考查了学生的化简运算能力及导数的计算.


科目:高中数学 来源: 题型:解答题
| 日销售量(本) | 小于100 | [100,200) | 大于等于200 |
| 奖励金额(元) | 0 | 100 | 200 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,点D在边AB上,CD⊥BC,AC=5$\sqrt{3}$,CD=5,BD=2AD.
如图,在△ABC中,点D在边AB上,CD⊥BC,AC=5$\sqrt{3}$,CD=5,BD=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 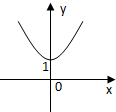 | B. | 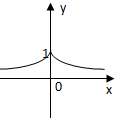 | C. |  | D. | 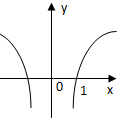 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com