

科目:高中数学 来源: 题型:
 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.
如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.查看答案和解析>>
科目:高中数学 来源: 题型:
 为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.
为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 4 |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
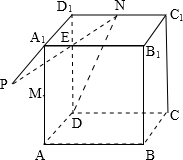 如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?
如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com