
(本题满分14分)如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角 始终为
始终为 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设 .
.

(Ⅰ)用t表示出PQ的长度,并探求 的周长l是否为定值;
的周长l是否为定值;
(Ⅱ)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)?
(1) =定值;
=定值;
(2)探照灯照射在正方形 内阴影部分的面积
内阴影部分的面积 最大为
最大为 平方百米.
平方百米.
解析试题分析:(1) 结合三角函数定义得到DQ的值。和勾股定理得到PQ的值,求解周长。
结合三角函数定义得到DQ的值。和勾股定理得到PQ的值,求解周长。
(2)根据间接法得到所求解的面积表达式,运用不等式的思想求解得到最值。
 ---2分
---2分 -------------------------------------------------4分
-------------------------------------------------4分 ---------------------6分
---------------------6分 =定值--------------------------------7分
=定值--------------------------------7分 -----------------------10分
-----------------------10分 --------------------------------------------------12分
--------------------------------------------------12分 -----------------------------------------13分
-----------------------------------------13分
所以探照灯照射在正方形 内阴影部分的面积
内阴影部分的面积 最大为
最大为 平方百米.----14分
平方百米.----14分
考点:本试题主要考查了利用三角函数的性质和三角函数的定义得到边长和面积的表示的运用。
点评:解决该试题的关键是能合理的设出变量表述各个边长,并能得到其面积的表示,结合均值不等式得到最值。


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数f(t)= 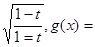
 ]
]
(Ⅰ)将函数g(x)化简成Asin(ωx+φ)+B(A>0,ω>0,φ∈[0,2π))的形式;
(Ⅱ)求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)已知函数
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com