Question

6．已知椭圆C：$\frac{x^2}{4}+\frac{y^2}{2}=1$的焦点分别为F₁，F₂．
（Ⅰ）求以线段F₁，F₂为直径的圆的方程；
（Ⅱ）过点P（4，0）任作一条直线l与椭圆C交于不同的两点M，N．在x轴上是否存在点Q，使得∠PQM+∠PQN=180°？若存在，求出点Q的坐标；若不存在，请说明理由．

Answer 1

分析 （ I）c²=2．然后求解以线段F₁F₂为直径的圆的方程．
（ II）若存在点Q（m，0），直线QM和QN的斜率存在，分别设为k₁，k₂．等价于k₁+k₂=0．设直线l的方程为y=k（x-4）．与椭圆方程联立，利用△＞0．求出${k^2}＜\frac{1}{6}$．设M（x₁，y₁），N（x₂，y₂），利用韦达定理，通过${k_1}+{k_2}=\frac{y_1}{{{x_1}-m}}+\frac{y_2}{{{x_2}-m}}=0$，求出m=1．说明存在点Q（1，0），使得∠PQM+∠PQN=180°．

解答 （本小题满分13分）
解：（ I）因为a²=4，b²=2，所以c²=2．
所以以线段F₁F₂为直径的圆的方程为x²+y²=2．…（3分）
（ II）若存在点Q（m，0），使得∠PQM+∠PQN=180°，
则直线QM和QN的斜率存在，分别设为k₁，k₂．
等价于k₁+k₂=0．
依题意，直线l的斜率存在，故设直线l的方程为y=k（x-4）．
由$\left\{{\begin{array}{l}{y=k（x-4）}\\{\frac{x^2}{4}+\frac{y^2}{2}=1}\end{array}}\right.$，得（2k²+1）x²-16k²x+32k²-4=0．
因为直线l与椭圆C有两个交点，所以△＞0．
即（16k²）²-4（2k²+1）（32k²-4）＞0，解得${k^2}＜\frac{1}{6}$．
设M（x₁，y₁），N（x₂，y₂），则${x_1}+{x_2}=\frac{{16{k^2}}}{{2{k^2}+1}}$，${x_1}{x_2}=\frac{{32{k^2}-4}}{{2{k^2}+1}}$，y₁=k（x₁-4），y₂=k（x₂-4）．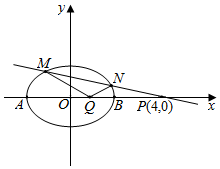

令${k_1}+{k_2}=\frac{y_1}{{{x_1}-m}}+\frac{y_2}{{{x_2}-m}}=0$，（x₁-m）y₂+（x₂-m）y₁=0，（x₁-m）k（x₂-4）+（x₂-m）k（x₁-4）=0，
当k≠0时，2x₁x₂-（m+4）（x₁+x₂）+8m=0，
所以$2×\frac{{32{k^2}-4}}{{2{k^2}+1}}$$-（m+4）×\frac{{16{k^2}}}{{2{k^2}+1}}+8m=0$，
化简得，$\frac{8（m-1）}{{2{k^2}+1}}=0$，
所以m=1．
当k=0时，也成立．
所以存在点Q（1，0），使得∠PQM+∠PQN=180°．…（14分）

点评 本题考查直线与椭圆的综合应用，考查转化思想的应用，存在性问题的处理方法，考查分析问题解决问题的能力．