
分析 (Ⅰ)去掉绝对值号,解关于a的不等式组,求出a的范围即可;(Ⅱ)通过讨论x的范围,结合基本不等式的性质求出求出f(x)的最小值即可.
解答 (Ⅰ)解:∵a<0,∴f(0)=|a|+|-$\frac{1}{a}$|=-a-$\frac{1}{a}$>$\frac{5}{2}$,
即a2+$\frac{5}{2}$a+1>0,
解得a<-2或-$\frac{1}{2}$<a<0;
(Ⅱ)证明:f(x)=|2x+a|+|x-$\frac{1}{a}$|=$\left\{\begin{array}{l}{3x+a-\frac{1}{a},x≥-\frac{a}{2}}\\{-x-a-\frac{1}{a},\frac{1}{a}<x<-\frac{a}{2}}\\{-3x-a+\frac{1}{a},x≤\frac{1}{a}}\end{array}\right.$,
当x≥-$\frac{a}{2}$时,f(x)≥-$\frac{a}{2}$-$\frac{1}{a}$;
当$\frac{1}{a}$<x<-$\frac{a}{2}$时,f(x)>-$\frac{a}{2}$-$\frac{1}{a}$;
当x≤$\frac{1}{a}$时,f(x)≥-a-$\frac{2}{a}$,
∴f(x)min=-$\frac{a}{2}$-$\frac{1}{a}$≥2$\sqrt{(-\frac{a}{2})(-\frac{1}{a})}$=$\sqrt{2}$,
当且仅当-$\frac{a}{2}$=-$\frac{1}{a}$即a=-$\sqrt{2}$时取等号,
∴f(x)≥$\sqrt{2}$.
点评 本题考查了基本不等式的性质,考查解绝对值不等式问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
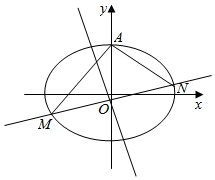 已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$
已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,1] | B. | (1,2) | C. | [1,2) | D. | (-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -5 | C. | 3 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com