

分析 (1)当E是PC中点时,OE∥平面PAD,取PD中点F,连接AF、EF、OF,证明四边形EFAO是平行四边形,然后证明OE∥平面ADP.
(2)过D作DH⊥AC交AC于点H,连接PH,说明∠PHD是二面角P-AC-D的平面角,判断四棱锥P-ABCD的外接球的直径即为PB,求解PB,然后求解四棱锥P-ABCD的外接球的表面积.
解答 解:(1)当E是PC中点时,OE∥平面PAD,
证明如下:取PD中点F,连接AF、EF、OF,
在△PDC中,E、F分别是PC、PD的中点,
∴EF是△PDC的中位线,
∴EF∥DC且$EF=\frac{1}{2}DC$,又O是AB中点,AB=DC,
∴EF∥AO且EF=AO,
∴四边形EFAO是平行四边形,
∴OE∥AF.
又∵AF?平面ADP,OE?平面ADP,
∴OE∥平面ADP.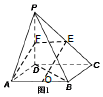
(2)由三视图可得PD⊥平面ABCD,
在底面ABCD中,过D作DH⊥AC交AC于点H,连接PH,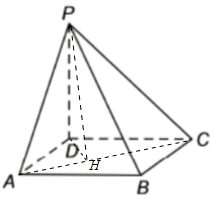
∵PD⊥平面ABCD,AC?平面ABCD,∴PD⊥AC,
又DH⊥AC,DH?平面ABCD,PD?平面ABCD,∵DH∩PD=D,∴AC⊥平面PD
又PH?平面PDH,∴PH⊥AC,
∴∠PHD是二面角P-AC-D的平面角,
在底面矩形ABCD,AB=8,AD=4,∴$AC=4\sqrt{5}$,$DH=\frac{8}{{\sqrt{5}}}$,
在Rt△PDH中,又$cos∠PHD=\frac{{\sqrt{6}}}{6}$,
∴$tan∠PHD=\frac{PD}{DH}=\sqrt{5}$,∴PD=8.
由直观图易知四棱锥P-ABCD的外接球的直径即为PB,
∴PB2=PD2+DB2=144.
故四棱锥P-ABCD的外接球的表面积为4πR2=144π.
点评 本题考查二面角的平面角的应用,直线与平面平行的判定定理的应用,外接球的表面积的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
 微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者.
微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 5 | C. | $\frac{9}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | [1,2) | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABC-A'B'C'为直三棱柱,M为CC的中点,N为AB的中点,AA'=BC=3,AB=2,AC=$\sqrt{13}$.
如图,ABC-A'B'C'为直三棱柱,M为CC的中点,N为AB的中点,AA'=BC=3,AB=2,AC=$\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{6}$a | B. | $\frac{\sqrt{6}}{3}$a | C. | $\frac{\sqrt{2}}{2}$a | D. | $\frac{1}{2}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com