考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得AB⊥BC1,C1B⊥BC,由此能证明C1B⊥平面ABC.
(2)以线段BB1为直径画圆O,分别交线段CC1于点E、C1.由已知条件推导出线段CC1的中点E即是要求的点.
(3)以B为原点,BC为x轴,BC1为y轴,BA为z轴,建立空间直角坐标系,利用向量法能求出二面角A-EB1-A1的平面角的正切值.
解答:
(1)证明:∵AB⊥侧面BB
1C
1C,∴AB⊥BC
1.
在△BC
1C中,BC=1,CC
1=BB
1=2,∠BCC
1=
,
由余弦定理得BC
1=
=
=
,
故有BC
2+BC
21=CC
21,∴C
1B⊥BC,
而BC∩AB=B且AB,BC?平面ABC,
∴C
1B⊥平面ABC.
(2)解:如图所示:
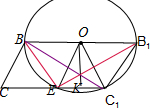
以线段BB
1为直径画圆O,分别交线段CC
1于点E、C
1.
下面说明点E、C
1是上述所画的圆与线段CC
1的交点.
①∵B
1C
1=OB
1=1,∠OB
1C=
,
∴△OB
1C
1是正三角形,∴OC
1=1,即点C
1在所画的圆上.
②作OK⊥CC
1,垂足为K,取EK=KC
1,则点E也在所画的圆上.
∵OE=OC
1=1,∴点E也在所画的圆上.
∵CC
1∥BB
1,∴∠OBE=∠OB
1C
1=
,
∴△OBE是正三角形,∴EB=1,
∴EB=BC=1,又∠BCE=
,∴△BCE为正三角形,
∴CE=1,即E点是线段CC
1的中点.
下面证明点E满足条件.
∵AB⊥侧面BB
1C
1C,B
1E⊥BE,
据三垂线定理可得B
1E⊥AE.
故线段CC
1的中点E即是要求的点.
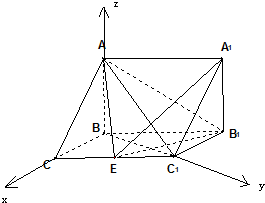
(3)解:以B为原点,BC为x轴,BC
1为y轴,BA为z轴,
建立空间直角坐标系,
A(0,0,
),E(1,1,0),B
1(0,2,0),A
1(0,2,
),
=(-1,-1,
),
=(-1,1,0),
=(-1,1,
),
设平面AEB
1的法向量
=(x,y,z),
则
,取x=1,得
=(1,1,
),
设平面A
1EB
1的法向量
=(a,b,c),
则
,取a=1,得
=(1,1,0),
cos<
,>=
=
,
∴二面角A-EB
1-A
1的平面角的正切值为1.
点评:本题考查直线与平面垂直的证明,考查满足条件的点的确定,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

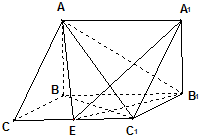 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1= 以线段BB1为直径画圆O,分别交线段CC1于点E、C1.
以线段BB1为直径画圆O,分别交线段CC1于点E、C1.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案