
 已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.| AD |
| BD |
| EC |
| CA |


科目:高中数学 来源: 题型:
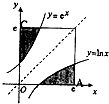 如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )
如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、d<0 | B、d>1 |
| C、d>1或d<0 | D、0<d<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
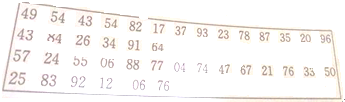 福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )
福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )| A、23 | B、09 | C、02 | D、17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com