
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
分析 (1)由表中数据的分散程度可得结论;
(2)由表中数据可得$\overline{x}$,$\overline{y}$,进而可得$\widehat{b}$和$\widehat{a}$,可得回归方程,令x=6可得预测值;
(3)列举可得总的基本事件有10个,符合题意的有6个,由概率公式可得.
解答 解:(1)由表中数据可知,甲的纯收入比乙的纯收入集中,故甲的纯收入较稳定;
(2)∵$\overline{x}$=$\frac{1}{5}$(1+2+3+4+5)=3,$\overline{y}$=$\frac{1}{5}$(2.9+3.3+3.6+4.4+4.8)=3.8,
$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2=10,
同理可得$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4.9,
∴$\widehat{b}$=$\frac{4.9}{10}$=0.49,$\widehat{a}$=3.8-0.49×3=2.33,
∴所求回归方程为$\widehat{y}$=0.49x+2.33,
令x=6可得$\widehat{y}$=0.49×6+2.33=5.27,
∴预测甲在6月份的纯收入为5.27千元;
(3)现从乙这5个月的纯收入中,随机抽取两个月的基本事件有:
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种,
记“恰有1个月的纯收入在区间(3,3.5)中”为事件A,则A包括的基本事件有:
(1,3),(1,4),(1,5),(2,3),(2,4),(2,5)共6种,
∴恰有1个月的纯收入在区间(3,3.5)中的概率为P(A)=$\frac{6}{10}$=$\frac{3}{5}$
点评 本题考查线性回归方程,涉及列举法求古典概型的概率,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
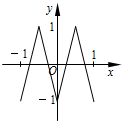 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )| A. | 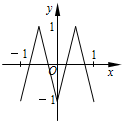 | B. | 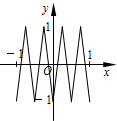 | C. | 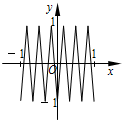 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
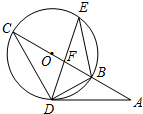 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com