
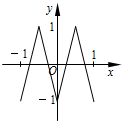 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )| A. | 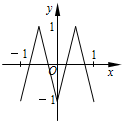 | B. | 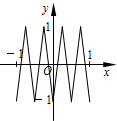 | C. | 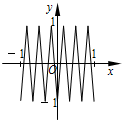 | D. |  |
分析 已知函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1 (x)=f[fn(x)],可以根据图象与x轴的交点进行判断,求出f1(x)的解析式,可得与x轴有两个交点,f2(x)与x轴有4个交点,以此来进行判断.
解答 解:函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1 (x)=f[fn(x)],
由图象可知f(x)为偶函数,关于y轴对称,所以只需考虑x≥0的情况即可:
由图f1(x)是分段函数,
函数f1(x)=f(x)=$\left\{\begin{array}{l}{4x-1,0≤x≤\frac{1}{2}}\\{-4x+3,\frac{1}{2}<x≤1}\end{array}\right.$,
是分段函数,
∵f2(x)=f(f(x)),
当0≤x≤$\frac{1}{2}$,f1(x)=4x-1,可得-1≤f(x)≤1,仍然需要进行分类讨论:
①0≤f(x)≤$\frac{1}{2}$,可得0<x≤$\frac{1}{4}$,此时f2(x)=f(f1(x))=4(4x-1)=16x-4,
②$\frac{1}{2}$≤f(x)≤1,可得$\frac{1}{4}$<x≤$\frac{1}{2}$,此时f2(x)=f(f1(x))=-4(4x-1)=-16x+4,
可得与x轴有2个交点;
当$\frac{1}{2}$≤x≤1,时,也分两种情况,此时也与x轴有两个交点;
∴f2(x)在[0,1]上与x轴有4个交点;
那么f3(x)在[0,1]上与x轴有6个交点;
∴f4(x)在[0,1]上与x轴有8个交点,同理在[-1.0]上也有8个交点,
故选:D.
点评 此题主要考查函数的图象问题,以及分段函数的性质及其图象,属于中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
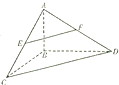 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
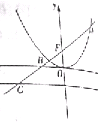 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com