
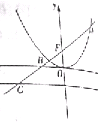
 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2. 分析 分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,根据抛物线定义可知|BD|=a,进而推断出∠BCD的值,求出|CF|,可得|GF|,即可求出p的值.
解答 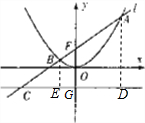 解:分别过点A,B作准线的垂线,分别交准线于点E,D,准线与y轴交点为G,
解:分别过点A,B作准线的垂线,分别交准线于点E,D,准线与y轴交点为G,
设|BF|=a,则由已知得:|BC|=$\sqrt{2}$a,由定义得:|BD|=a,故∠BCD=45°,
在直角三角形ACE中,∵|AE|=4+2$\sqrt{2}$,
∴|AC|=4$\sqrt{2}$+4
∵|AF|=4+2$\sqrt{2}$,
∴|CF|=2$\sqrt{2}$,
∴|GF|=2
∴p=2,
故答案为:2.
点评 本题主要考查了抛物线的标准方程.考查了学生对抛物线的定义和基本知识的综合把握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
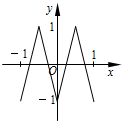 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )| A. | 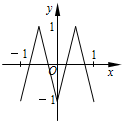 | B. | 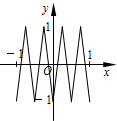 | C. | 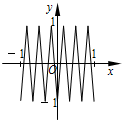 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com