
分析 由$\frac{1+tan(π+α)}{1+tan(2π-α)}$=-3运用诱导公式化简求值可得tanα=2,由诱导公式,倍角公式,万能公式化简所求即可得解.
解答 解:∵$\frac{1+tan(π+α)}{1+tan(2π-α)}$=-3⇒$\frac{1+tanα}{1-tanα}$=-3⇒1+tanα=-3+3tanα⇒tanα=2,
∴cos2(π-α)+sin($\frac{3π}{2}$+α)•cos($\frac{π}{2}$+α)+2sin2(α-π)
=cos2α+cosα•sinα+2sin2α
=1+$\frac{1-cos2α}{2}$+$\frac{1}{2}$sin2α
=$\frac{3}{2}$+$\frac{1}{2}$(sin2α-cos2α)
=$\frac{3}{2}$+$\frac{1}{2}×\frac{2tanα}{1+ta{n}^{2}α}$-$\frac{1}{2}×\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$
=$\frac{3}{2}$+$\frac{1}{2}×\frac{4}{5}$-$\frac{1}{2}×\frac{-3}{5}$
=$\frac{11}{5}$.
点评 本题主要考查了运用诱导公式化简求值,同角三角函数基本关系的运用,熟练使用相关公式是解题的关键,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
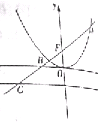 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
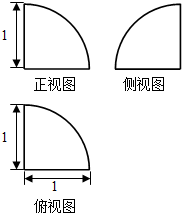
| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com