
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 当n→+∞时,直线2x-y=$\frac{n}{n+1}$趋近于2x-y=1,与圆x2+y2=2在第一象限的交点无限靠近(1,1),利用圆的切线的斜率、斜率计算公式即可得出.
解答 解:当n→+∞时,直线2x-y=$\frac{n}{n+1}$趋近于2x-y=1,与圆x2+y2=2在第一象限的交点无限靠近(1,1),而$\frac{{y}_{n}-1}{{x}_{n}-1}$可看作点 Pn(xn,yn)与(1,1)连线的斜率,其值会无限接近圆x2+y2=2在点(1,1)处的切线的斜率,其斜率为-1.
∴$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=-1.
故选:A.
点评 本题考查了极限思想、圆的切线的斜率、斜率计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
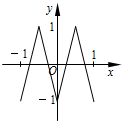 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )| A. | 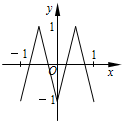 | B. | 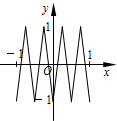 | C. | 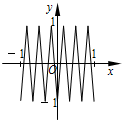 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
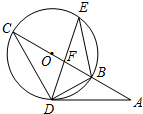 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com