
| A. | ②③ | B. | ①② | C. | ①②④ | D. | ①②③ |
分析 化简函数的解析式,结合函数的图象的特征,判断此函数是否有自公切线.
解答 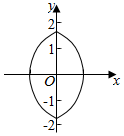 解:①、y=x2-|x|+1=$\left\{\begin{array}{l}{(x-\frac{1}{2})^{2}+\frac{3}{4},x≥0}\\{(x+\frac{1}{2})^{2}+\frac{3}{4},x<0}\end{array}\right.$,在x=$\frac{1}{2}$和x=-$\frac{1}{2}$ 处的切线都是y=$\frac{3}{4}$,故有自公切线.
解:①、y=x2-|x|+1=$\left\{\begin{array}{l}{(x-\frac{1}{2})^{2}+\frac{3}{4},x≥0}\\{(x+\frac{1}{2})^{2}+\frac{3}{4},x<0}\end{array}\right.$,在x=$\frac{1}{2}$和x=-$\frac{1}{2}$ 处的切线都是y=$\frac{3}{4}$,故有自公切线.
②、y=3sinx+4cosx=5sin(x+φ),cosφ=$\frac{3}{5}$,sinφ=$\frac{4}{5}$,
此函数是周期函数,过图象的最高点的切线都重合,故此函数有自公切线.
③、$y=x+\frac{1}{x}$为对勾函数,分别位于一三象限,图象关于原点对称且导数为
y′=1-$\frac{1}{{x}^{2}}$,在(-∞,-1),(1,+∞)递增,(-1,0),(0,1)递减,存在平行的切线,不存在自公切线;
④、由于|x|+1=$\sqrt{4-{y}^{2}}$,即 x2+2|x|+y2-3=0,结合图象可得,此曲线没有自公切线.
故选:B.
点评 本题考查函数的自公切线的定义,函数图象的特征,准确判断一个函数是否有自公切线,是解题的难点.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
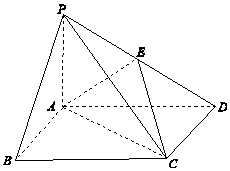 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | m=-1 | C. | m>-1 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com