
分析 解x2+4x=0可得集合A,由B⊆A,进而可得B=∅或{0}或{-4}或{0,-4},分别求出a的值,综合可得答案
解答 解:A={x|x2+4x=0,x∈R}={0,-4},
∵B⊆A,
∴B=∅或{0}或{-4}或{0,-4};
①当B=∅时,△=[2(a+1)]2-4•(a2-1)<0⇒a<-1,
②当B={0}时,$\left\{\begin{array}{l}{0=-2(a+1)}\\{0={a}^{2}-1}\end{array}\right.$⇒a=-1,
③当B={-4}时,$\left\{\begin{array}{l}{-4-4=-2(a+1)}\\{16={a}^{2}-1}\end{array}\right.$⇒a不存在,
④当B={0,-4}时,$\left\{\begin{array}{l}{-4+0=-2(a+1)}\\{0={a}^{2}-1}\end{array}\right.$⇒a=1,
∴a的取值范围为(-∞,-1]∪{1}.
点评 本题考查集合间的相互关系,涉及参数的取值问题,注意分析B=∅的情况.


科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,+∞) | C. | ($\frac{2}{3}$,+∞) | D. | (11,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
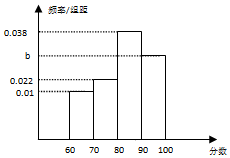 某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:| 分组 | 频数 | 频率 |
| [60,70) | 10 | 0.1 |
| [70,80) | 22 | 0.22 |
| [80,90) | a | 0.38 |
| [90,100] | 30 | c |
| 合计 | 100 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(1,\sqrt{2})$ | D. | $\sqrt{2},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com