
 =4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
=4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。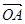 ·
·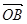 的值;(2)设
的值;(2)设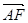 =
=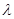
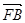 ,求△ABO的面积S的最小值;
,求△ABO的面积S的最小值;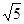 ,求
,求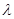 的取值范围。
的取值范围。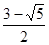 ≦
≦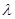 ≦
≦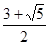
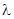 的表达式,进而结合不等式的思想得到最值。
的表达式,进而结合不等式的思想得到最值。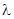 的范围。
的范围。 -4my-4=0.
-4my-4=0.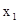 ,
,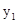 ),(
),(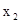 ,
,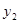 )(
)(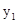 ﹥0﹥
﹥0﹥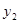 ),则
),则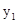
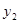 =-4.
=-4.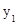
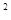 =4
=4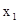 ,
,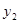
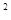 =4
=4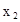 ,所以
,所以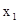
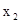 =
=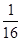
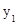
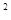
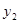
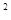 =1,
=1,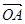 ·
·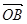 =
=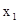
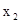 +
+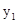
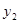 =-3 ………………………………………………4分
=-3 ………………………………………………4分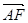 =
=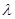
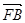 ,所以(1-
,所以(1-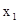 ,-
,-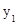 )=
)=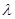 (
(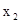 -1,
-1,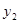 )即 1-
)即 1-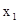 =
=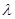
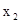 -
-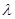 ①
①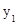 =
=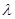
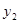 ②
②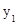
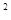 =4
=4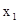 ③
③ 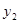
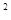 =4
=4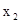 ④ ,由②③④消去
④ ,由②③④消去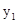 ,
,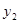 后,得到
后,得到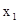 =
=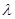
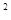
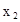 ,将其代入①,注意到
,将其代入①,注意到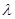 ﹥0,解得
﹥0,解得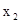 =
=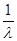 。
。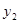 =-
=-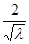 ,
,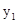 =2
=2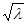 ,故△OAB的面积S=
,故△OAB的面积S=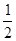
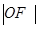 ·
·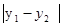 =
=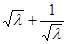
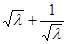 ≧2恒成立,故△OAB的面积S的最小值是2………(8分).(3)由
≧2恒成立,故△OAB的面积S的最小值是2………(8分).(3)由 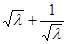 ≦
≦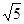 解之的
解之的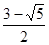 ≦
≦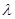 ≦
≦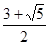 ………………………………………………12分
………………………………………………12分

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
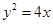 的焦点为
的焦点为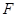 ,过点
,过点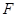 的直线交抛物线于
的直线交抛物线于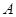 ,
,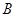 两点.
两点.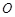 为坐标原点,求证:
为坐标原点,求证: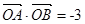 ;
;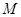 在线段
在线段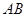 上运动,原点
上运动,原点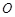 关于点
关于点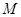 的对称点为
的对称点为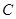 ,求四边形
,求四边形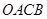 面积的最小值..
面积的最小值..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
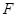 是抛物线
是抛物线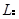
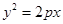
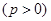 的焦点,
的焦点,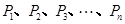 是抛物线
是抛物线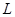 上的
上的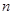 个不同的点(
个不同的点(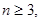
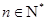 ).
).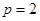 时,试写出抛物线
时,试写出抛物线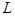 上的三个定点
上的三个定点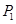 、
、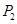 、
、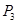 的坐标,从而使得
的坐标,从而使得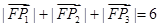 ;
;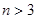 时,若
时,若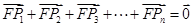 ,
, ;
;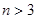 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即: ,则
,则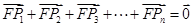 .”
.”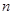 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
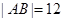 ,P为C的准线上一点,则
,P为C的准线上一点,则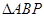 的面积为( )
的面积为( )| A.18 | B.24 | C. 36 | D. 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com