
分析 直接利用弦切互化以及二倍角公式化简求解即可.
解答 解:$\frac{{1+\sqrt{3}tan{{50}°}}}{{\sqrt{1-cos{{100}°}}}}$
=$\frac{1+\frac{\sqrt{3}sin50°}{cos50°}}{\sqrt{1-1+2si{n}^{2}50°}}$
=$\frac{cos50°+\sqrt{3}sin50°}{\sqrt{2}sin50°cos50°}$
=$\frac{\sqrt{2}(\frac{1}{2}cos50°+\frac{\sqrt{3}}{2}sin50°)}{\frac{1}{2}sin100°}$
=$\frac{2\sqrt{2}sin(30°+50°)}{cos10°}$
=2$\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 本题考查二倍角公式以及两角和与差的三角函数,诱导公式的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}cos1$ | B. | $-\sqrt{3}cos1$ | C. | $\sqrt{3}sin1$ | D. | $-\sqrt{3}sin1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
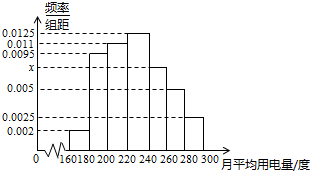
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 3 | 4 | 8 | 15 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 1 | 2 | 8 | 9 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com