
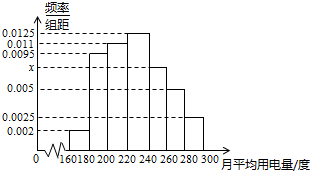
分析 (Ⅰ)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,解方程可得;
(Ⅱ)可得各段的用户分别为25,15,10,5,可得抽取比例,可得要抽取的户数;
(Ⅲ)由直方图可得中位数在[220,240)内,设中位数为a,解方程(0.002+0.0095++0.011)×20+0.0125×(a-220)=0.5可得.
解答 解:(Ⅰ)由直方图的性质可得:
(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,
解方程可得x=0.0075,
∴直方图中x的值为0.0075; (4分)
(Ⅱ)月平均用电量为[220,240)的用户有0.0125×20×100=25,
月平均用电量为[240,260)的用户有0.0075×20×100=15,
月平均用电量为[260,280)的用户有0.005×20×100=10,
∴月平均用电量在[220,240)的用户中应抽取$10×\frac{25}{25+15+10}=5$户.(8分)
(Ⅲ)∵(0.002+0.0095+0.011)×20=0.45<0.5,
∴月平均用电量的中位数在[220,240)内,设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5可得a=224,
∴月平均用电量的中位数为224; (12分)
点评 本题考查频率分布直方图,涉及众数和中位数以及分层抽样,属基础题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 246 | B. | 258 | C. | 280 | D. | 270 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com