
分析 (1)根据平面向量的数量积公式得出f(x)并用二倍角公式化简,使用周期公式得出周期;
(2)利用正弦函数的单调性列出不等式解出;
(3)根据函数图象平移规律得出;
(4)令f(x0)=±1,结合x0的范围求出x0.
解答 解:(1)f(x)=2$\sqrt{3}$sinxcosx+2cos2x-1=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$).
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,解得$\frac{π}{6}+2kπ$≤x≤$\frac{2π}{3}+2kπ$,
∴函数f(x)的单调递减区间是[$\frac{π}{6}+2kπ$,$\frac{2π}{3}+2kπ$].
(3)f(x)=2sin2(x+$\frac{π}{12}$).
∴f(x)可看做是由y=sin2x的图象先向左平移$\frac{π}{12}$个单位,再保持横坐标不变,纵坐标扩大到原来的2倍得到的.
(4)∵f(x)的图象关于x=x0对称,∴f(x0)=±1,
∴2x0+$\frac{π}{6}$=$\frac{π}{2}$+kπ,解得x0=$\frac{π}{6}$+$\frac{kπ}{2}$.∵0<x0<$\frac{π}{2}$,∴x0=$\frac{π}{6}$.
点评 本题考查了平面向量的数量积公式,三角函数恒等变换,正弦函数的性质,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $4\sqrt{2}$ | C. | 4 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
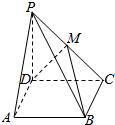 已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.
已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3} | B. | {-1,2} | C. | {-3,-1,2} | D. | {-3,-1,2,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com