Question

5．已知x₁是函数f（x）=log${\;}_{\frac{1}{2}}$x-（$\frac{1}{2}$）^x的零点，x₂是函数g（x）=log₂x-（$\frac{1}{2}$）^x的零点，则x₁x₂的取值范围是（0，1）．

Answer 1

分析 根据函数零点的性质，确定两个零点的取值范围，结合指数函数和对数函数的单调性，即可得到结论．

解答 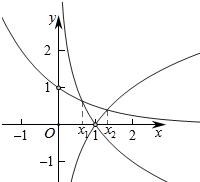解：∵x₁是函数f（x）=log${\;}_{\frac{1}{2}}$x-（$\frac{1}{2}$）^x的零点，x₂是函数g（x）=log₂x-（$\frac{1}{2}$）^x的零点，
∴log${\;}_{\frac{1}{2}}$x₁=$（\frac{1}{2}）^{{x}_{1}}$，和log₂x₂=（$\frac{1}{2}$）${\;}^{{x}_{2}}$，
则由图象可知，0＜x₁＜1，x₂＞1，∴x₁＜x₂，
则两式相减得$（\frac{1}{2}）^{{x}_{1}}$-（$\frac{1}{2}$）${\;}^{{x}_{2}}$=log₂x₁-$log_{\frac{1}{2}}}$x₂=log₂x₁+log₂x₂=log₂x₁x₂＜0
即0＜x₁x₂＜1，
故答案为：（0，1）．

点评 本题主要考查函数零点的应用，利用数形结合，以及指数函数和对数函数的单调性的性质是解决本题的关键．