练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．函数f（x）=$\left\{\begin{array}{l}{ax+b，x＜-1}\\{ln（x+a），x≥-1}\\{\;}\end{array}\right.$的图象如图所示，则f（-3）等于（　　）
    A．-$\frac{1}{2}$B．-$\frac{5}{4}$C．-1D．-2

    分析 由条件利用函数的图象可得a（-1）+b=3，ln（-1+a）=0，由此求得a、b的值，从而求得f（-3）的值．

    解答 解：根据函数f（x）=$\left\{\begin{array}{l}{ax+b，x＜-1}\\{ln（x+a），x≥-1}\\{\;}\end{array}\right.$的图象，可得a（-1）+b=3，ln（-1+a）=0，
    求得a=2，b=5，∴f（x）=$\left\{\begin{array}{l}{2x+5，x＜-1}\\{ln（x+2），x≥-1}\end{array}\right.$，f（-3）=2•（-3）+5=-1，
    故选：C．

    点评 本题主要考查分段函数的应用，求函数的解析式、求函数的值，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

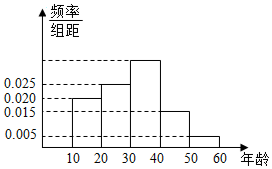    10．随机抽取100名年龄在[10，20），[20，30）…，[50，60）年龄段的市民进行问卷调查，由此得到样本的频率分布直方图如图所示，从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人，则在[50，60）年龄段抽取的人数为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．若椭圆的两焦点与短轴两端点在单位圆上，则此椭圆的内接正方形的边长为$\frac{2\sqrt{6}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．等比数列{an}中，a1=1，公比q=2，前n项和为Sn，下列结论正确的是（　　）
    A．$?{n_0}∈N*，{a_{n_0}}+{a_{{n_0}+2}}=2{a_{{n_0}+1}}$
    B．?n∈N*，an•an+1≤an+2
    C．?n∈N*，Sn＜an+1
    D．$?{n_0}∈N*，{a_{n_0}}+{a_{{n_0}+3}}={a_{{n_0}+1}}+{a_{{n_0}+2}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若实数x，y满足$\left\{\begin{array}{l}x+y-1≤0\\ 2x-y-2≤0\\ y≤1.\end{array}\right.$，则目标函数z=x-3y的最小值为（　　）
    A．0B．1C．$-\frac{3}{2}$D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：
    （1）成绩在180分以上者到甲部门工作，180分以下者到乙部门工作；（2）只有成绩不低于190分的才能担任助理工作．
    （Ⅰ）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，甲部门中至多有多少女生入选？
    （Ⅱ）若公司选2人担任助理工作，估计几名女生入选的可能性最大？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，其中|$\overrightarrow{a}$|=$\sqrt{3}$，|$\overrightarrow{b}$|=2，且（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角是$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．所示的程序框图输出的结果为S=35，则判断框中应填入的关于k的条件是（　　）
    A．k＞7B．k≤6C．k＞6D．k＜6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知O是△ABC内一点，∠AOB=150°，∠AOC=120°，且|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=3，若m$\overrightarrow{OA}$+n$\overrightarrow{OB}$=$\overrightarrow{OC}$，则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$|=$\sqrt{8-2\sqrt{3}}$，m+$\sqrt{3}$n的值是-12．

    查看答案和解析>>

    同步练习册答案