练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

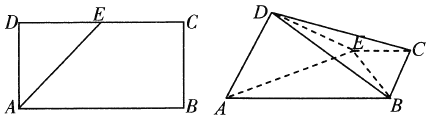
    【题目】如图，在矩形中，，，是的中点.将沿折起，使折起后平面平面，则异面直线和所成角的余弦值为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    由题意，取AB中点F，连接CF，则CF∥AE，可得直线AE和CD所成角的平面角为∠DCF，结合已知求解△DCF三边长度，满足直角三角形，可得cos∠DCF.

    由题意，

    取AB中点F，连接CF，则CF∥AE，可得直线AE和CD所成角的平面角为∠DCF，（如图）

    过D作DM垂直AE于M，平面DAE⊥平面ABCE，

    AD＝DE，

    ∴DM⊥AE，

    ∴DM⊥平面ABCE，∴DM⊥MF，

    且AM＝DM，结合平面图形可得：FM=, ∴DF==1,CF=,

    又=, ∴=3,

    ∴在△DFC中，=,

    ∴△DFC是直角三角形且DF⊥FC，

    可得cos∠DCF．

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设点是抛物线上的动点，是的准线上的动点，直线过且与（为坐标原点）垂直，则点到的距离的最小值的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，平面，为边上一点，，.

    （1）证明：平面平面.

    （2）若，试问：是否与平面平行？若平行，求三棱锥的体积；若不平行，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中正确的是（ ）

    A. “”是“”成立的充分不必要条件

    B. 命题，则

    C. 为了了解800名学生对学校某项教改试验的意见，用系统抽样的方法从中抽取一个容量为40的样本，则分组的组距为40

    D. 已知回归直线的斜率的估计值为1.23，样本点的中心为，则回归直线方程为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨)标准煤的几组对照数据

    (1)请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    (2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点A(-4，2)是Rt△的直角顶点，点O是坐标原点，点B在x轴上.

    (1)求直线AB的方程;

    (2)求△OAB的外接圆的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在平面直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，点的极坐标为，斜率为的直线经过点.

    （I）求曲线的普通方程和直线的参数方程；

    （II）设直线与曲线相交于，两点，求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:

    表1：红粒高粱频数分布表

    农作物高度()

    频 数

    2

    5

    14

    13

    4

    2

    表2：白粒高粱频数分布表

    农作物高度()

    频 数

    1

    7

    12

    6

    3

    1

    (1)估计这700棵高粱中红粒高粱的棵数;

    (2)估计这700棵高粱中高粱高()在的概率；

    (3)在样本的红粒高粱中，从高度(单位：)在中任选3棵，设表示所选3棵中高(单位：)在的棵数，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，四边形为正方形，，，.

    （1）证明：平面平面.

    （2）若平面，二面角为，三棱锥的外接球的球心为，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案