
分析 (1)由题意,过M,F,O三点的圆的圆心为N,点N到抛物线C的准线的距离为$\frac{3}{4}$,可得$\frac{p}{2}$+$\frac{p}{4}$=$\frac{3}{4}$,求出p,即可求抛物线C的方程;
(2)设点Q(x,y),A(x1,y1),B(x2,y2),设$\overrightarrow{AP}$=-λ$\overrightarrow{AQ}$,$\overrightarrow{PB}$=λ$\overrightarrow{QB}$(0<λ<1),于是x1=$\frac{4-λx}{1-λ}$,y1=$\frac{1-λy}{1-λ}$,x2=$\frac{4+λx}{1+λ}$,y2=$\frac{1+λy}{1+λ}$,又点A、B在抛物线C上,即x12=2y1,x22=2y2,代入相减能证明点Q总在直线上.
解答 (1)解:由题意,过M,F,O三点的圆的圆心为N,点N到抛物线C的准线的距离为$\frac{3}{4}$,
∴$\frac{p}{2}$+$\frac{p}{4}$=$\frac{3}{4}$,∴p=1,
∴抛物线C的方程为x2=2y;
(2)证明:设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题设|$\overrightarrow{AP}$|•|$\overrightarrow{QB}$|=|$\overrightarrow{AQ}$|•|$\overrightarrow{PB}$|,A,P,B,Q四点共线,可得$\overrightarrow{AP}$=-λ$\overrightarrow{AQ}$,$\overrightarrow{PB}$=λ$\overrightarrow{QB}$(0<λ<1),
于是x1=$\frac{4-λx}{1-λ}$,y1=$\frac{1-λy}{1-λ}$,x2=$\frac{4+λx}{1+λ}$,y2=$\frac{1+λy}{1+λ}$
又点A、B在抛物线C上,即x12=2y1,x22=2y2,
代入相减得4x-y-1=0,
即点Q(x,y)总在定直线4x-y-1=0上.
点评 本题综合考查抛物线方程与定比分点定理,同时考查构造消元处理方程组的能力.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
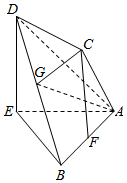 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com