考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)在数列递推式中取n=n-1得另一递推式,作差后可得{a
n}为以a
1=2为首项,以2为公差的等差数列,代入等差数列的通项公式得答案;
(2)把数列{a
n}的通项公式代入b
n+1-b
n=2a
n+3=4n+3,由叠加法得到数列{b
n}的通项公式,进一步得到
=<=-.
验证n=1,n=2,n=3满足T
n<
;当n≥4时放缩后利用裂项相消法求和后得答案.
解答:
解:(1)由
Sn=nan-(n2-n),得
Sn-1=(n-1)an-1-[(n-1)2-(n-1)](n≥2),
两式相减得:a
n-a
n-1=2(n≥2),
∴{a
n}为以a
1=2为首项,以2为公差的等差数列,
∴a
n=2+2(n-1)=2n;
(2)b
n+1-b
n=2a
n+3=4n+3,
叠加b
n=b
1+(b
2-b
1)+(b
3-b
2)+…(b
n-b
n-1)
=3+7+11+…(4n-1)=
=n(2n+1)(n≥2).
经检验b
1=3也符合,∴b
n=n(2n+1)
∴
=<=-.
当n=1时,
Tn=<;
当n=2时,
Tn=+=+=<;
当n=3时,
Tn=++=<;
当n≥4时,
Tn=+++…<+++-+-+…+
-=
-<.
综上所述
Tn<.
点评:本题考查了数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的和,考查了放缩法证明数列不等式,是中高档题.



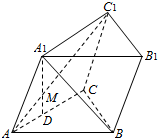 如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.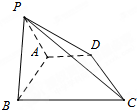 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=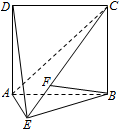 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.