
分析 (1)①利用相互独立事件的概率公式运算求得结果.
②由于每次摸出一个红球的概率都是$\frac{1}{3}$,即可求出第一次、第三次、第五次摸到红球的概率.
(2)设袋子A中有m个球,袋子B中有2m个球,由$\frac{{\frac{1}{3}m+2mp}}{3m}=\frac{2}{5}$,求得p的值.
解答 解:(1)①由于每次摸出一个红球的概率是$\frac{1}{3}$,摸不到红球的概率为$\frac{2}{3}$,故恰好有3次摸到红球的概率$C_5^3×{({\frac{1}{3}})^3}×{({\frac{2}{3}})^2}=\frac{40}{243}$.
②由于每次摸出一个红球的概率都是$\frac{1}{3}$,故第一次、第三次、第五次摸到红球的概率为${({\frac{1}{3}})^3}=\frac{1}{27}$.
(Ⅱ)设袋子A中有m个球,袋子B中有2m个球,
由$\frac{{\frac{1}{3}m+2mp}}{3m}=\frac{2}{5}$,得$p=\frac{13}{30}$
点评 本题主要考查相互独立事件的概率乘法公式、及n次独立重复试验中恰好发生k次的概率公式的应用,属于中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
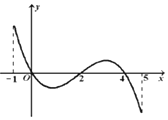 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 4 |
| f(x) | 1 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 24-π | B. | 24-3π | C. | $8-\frac{4π}{3}$ | D. | $8-\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 4 | C. | -4$\sqrt{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
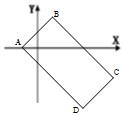 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2}$ | B. | 2017 | C. | $\frac{2018}{2}$ | D. | 2018 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com