
【题目】在三棱锥![]() 中,
中,![]() ,若平面
,若平面![]() 平面
平面![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为_______.
外接球的表面积为_______.
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为![]() ,且过点
,且过点![]() .点M(3,m)在双曲线上.
.点M(3,m)在双曲线上.
(1)求双曲线的方程;
(2)求证:![]() ;
;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在观察物体时,从物体上、下沿引出的光线在人眼处所成的夹角叫视角.研究表明,视角在![]() 范围内视觉效果最佳.某大广场竖立的大屏幕,屏幕高为20米,屏幕底部距离地面11.5米.站在大屏幕正前方,距离屏幕所在平面
范围内视觉效果最佳.某大广场竖立的大屏幕,屏幕高为20米,屏幕底部距离地面11.5米.站在大屏幕正前方,距离屏幕所在平面![]() 米处的某人,眼睛位置距离地面高度为1.5米,观察屏幕的视角为
米处的某人,眼睛位置距离地面高度为1.5米,观察屏幕的视角为![]() (情景示意图如图所示).
(情景示意图如图所示).
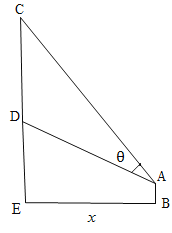
(1)为探究视觉效果,请从![]() ,
,![]() ,
,![]() 中选择一个作为
中选择一个作为![]() ,并求
,并求![]() 的表达式;
的表达式;
(2)根据(1)的选择探究![]() 是否有达到最佳视角效果的可能.
是否有达到最佳视角效果的可能.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB![]() EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
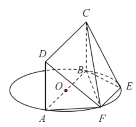
(I)求证:平面DAF⊥平面CBF;
(II)若BC=1,求四棱锥F-ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com