
分析 由已知得到($\overrightarrow{CA}$+$\overrightarrow{CB}$)•($\overrightarrow{CB}-\overrightarrow{CA}$)=${\overrightarrow{CB}}^{2}-{\overrightarrow{CA}}^{2}$=$\frac{2}{3}$|$\overrightarrow{AB}$|2,得到三角形的三边关系,结合余弦定理以及三角函数求出.
解答 解:由已知($\overrightarrow{CA}$+$\overrightarrow{CB}$)•$\overrightarrow{AB}$=$\frac{2}{3}$|$\overrightarrow{AB}$|2,所以($\overrightarrow{CA}$+$\overrightarrow{CB}$)•($\overrightarrow{CB}-\overrightarrow{CA}$)=${\overrightarrow{CB}}^{2}-{\overrightarrow{CA}}^{2}$=$\frac{2}{3}$|$\overrightarrow{AB}$|2,即CB2=CA2+$\frac{2}{3}$AB2,
又BC2=AB2+AC2-2AB×ACcosA,
所以CA2+$\frac{2}{3}$AB2=AB2+AC2-2AB×ACcosA,整理得$\frac{1}{6}$AB=ACcosA,
设AB边上的高为CD,则AD=ACcosA,
所以BD=5AD,所以$\frac{tanA}{tanB}$=$\frac{BD}{AD}$=5.
故答案为:5.
点评 本题考查了平面向量与余弦定理相结合的三角形问题;关键是由已知得到三角形三边关系.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 5种 | B. | 20种 | C. | 24种 | D. | 120种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=2sin(2x+\frac{π}{6})+1+a$,x∈[0,π]的最大值为2
已知函数$f(x)=2sin(2x+\frac{π}{6})+1+a$,x∈[0,π]的最大值为2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
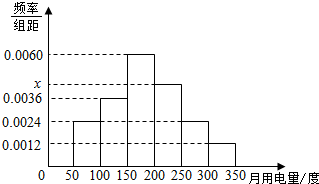 为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com