
分析 (1)利用和差公式即可得出.
(2)由sinθ+2cosθ=0,得sinθ=-2cosθ,可得tanθ=-2,再利用同角三角函数基本关系式、倍角公式即可得出.
解答 解:(1)cos25°cos35°-cos65°cos55°=sin30°=$\frac{1}{2}$,
(2)由sinθ+2cosθ=0,得sinθ=-2cosθ,又cosθ≠0,则tanθ=-2,
∴$\frac{cos2θ-sin2θ}{{1+{{cos}^2}θ}}=\frac{{{{cos}^2}θ-{{sin}^2}θ-2sinθcosθ}}{{{{sin}^2}θ+2{{cos}^2}θ}}$=$\frac{{1-{{tan}^2}θ-2tanθ}}{{{{tan}^2}θ+2}}=\frac{{1-{{(-2)}^2}-2(-2)}}{{{{(-2)}^2}+2}}=\frac{1}{6}$.
点评 本题考查了同角三角函数基本关系式、倍角公式、和差公式,考查了推理能力与计算能力,属于中档题.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
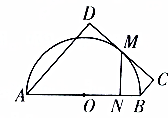 如图:已知AB为圆O的直径,直线CD与圆O相切与M,AD⊥CD于D,BC⊥CD于C,MN⊥AB于N,AD=3,BC=1.
如图:已知AB为圆O的直径,直线CD与圆O相切与M,AD⊥CD于D,BC⊥CD于C,MN⊥AB于N,AD=3,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com