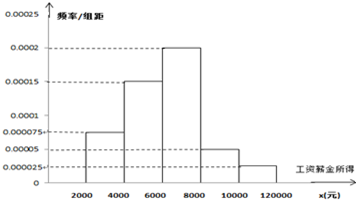
某市共有100万居民的月收入是通过“工资薪金所得”得到的,如图是抽样调查后得到的工资薪金所得X的频率分布直方图.工资薪金个人所得税税率表如表所示.表中“全月应纳税所得额”是指“工资薪金所得”减去3500元所超出的部分(3500元为个税起征点,不到3500元不缴税).
工资个税的计算公式为:“应纳税额”=“全月应纳税所得额”乘以“适用税率”减去“速算扣除数”.
| 全月应纳税所得额 |
适用税率(%) |
速算扣除数 |
| 不超过1500元 |
3 |
0 |
| 超过1500元至4500元 |
10 |
105 |
| 超过4500元至9000元 |
20 |
555 |
| … |
… |
… |
例如:某人某月“工资薪金所得”为5500元,则“全月应纳税所得额”为5500-3500=2000元,应纳税额为2000×10%-105=95(元)
在直方图的工资薪金所得分组中,以各组的区间中点值代表该组的各个值,工资薪金所得落入该区间的频率作为x取该区间中点值的概率
(Ⅰ)试估计该市居民每月在工资薪金个人所得税上缴纳的总税款;
(Ⅱ)设该市居民每月从工资薪金所得交完税后,剩余的为其月可支配额y(元),试求该市居民月可支配额不超过7000元的概率.



