考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)令n=1可求a1=2,当n≥2时,由an=Sn-Sn-1可得递推式,由递推式可判断该数列为等比数列,得到通项公式;
(2)由(1)可求bn,利用分组求和及错位相减法可求Tn,由(1)可得Sn,代入不等式,分离出t后转化为求函数的最值即可;
解答:
解:(1)当n=1时,a
1=2a
1-2,解得a
1=2;
当n≥2时,a
n=S
n-S
n-1=2a
n-2-(2a
n-1-2)=2a
n-2a
n-1,
∴a
n=2a
n-1,
故数列{a
n}是以a
1=2为首项,2为公比的等比数列,
故
an=2•2n-1=2
n.
(2)由(1)得,
bn=n•2n+log2n=n•2
n-n,
∴T
n=b
1+b
2+…+b
n=(2+2•2
2+3•2
3+…+n•2
n)-(1+2+…+n),
令
Rn=2+2•22+3•23+…+n•2
n,
则
2Rn=22+2•23+3•24+…+n•2
n+1,
两式相减得-
Rn=2+22+23+…+2n-n•2
n+1=
-n•2n+1,
∴
Rn=(n-1)2n+1+2,
故T
n=b
1+b
2+…+b
n=(n-1)2
n+1+2-
,
又由(1)得,S
n=2a
n-2=2
n+1-2,
不等式(n-1)(S
n+2)-T
n<t+
n
2 即为(n-1)2
n+1-(n-1)2
n+1-2+
<t+
n2,即为t>-
n2+n-2对任意n∈N
*恒成立,
设f(n)=-
n2+n-2,则f(n)=-
(n-)2-,
∵n∈N
*,∴f(n)
max=f(3)=-
,
故实数t的取值范围是(-
,+∞).
点评:该题考查由数列递推式求数列通项、等差数列的通项公式及数列求和,考查学生的运算求解能力、推理论证能力,错位相减法是数列求和的常用方法,要熟练.



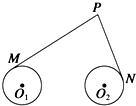 如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=
如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=