练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设等差数列{an}的前n项和为Sn，且满足S2013＞0，S2014＜0，则前n项和Sn取最大值时n的值为（　　）
    A．1009B．1008C．1007D．1006

    分析 由题意得数列{an}的前1008项均为正数，从1009项开始为负值，由此能求出n为1008时，Sn取最大值．

    解答 解：∵等差数列{an}的前n项和为Sn，且满足S2013＞0，S2014＜0，
    ∴由题意得，${S_{2015}}=\frac{{2015×（{a_1}+{a_{2015}}）}}{2}=\frac{{2015×2{a_{1008}}}}{2}$＞0，
    ∴数列{an}的前1008项均为正数，
    又∵S2016＜0，故从1009项开始为负值，
    故n为1008时，Sn取最大值．
    故选：B．

    点评 本题考查等差数列的前n项和最大时，项数n的求不地，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

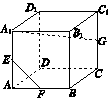    16．如图所示，在正方体ABCD-A1B1C1D1中，AA1，AB，CC1的中点分别为E，F，G，则EF与A1G所成的角为（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数g（x）=ax2-2ax+1+b（a＞0）在区间[2，3]上的最大值为4，最小值为1，记f（x）=g（|x|），x∈R；
    （1）求实数a、b的值；
    （2）若不等式$f（x）+g（x）≥log_2^2k-2{log_2}k-3$对任意x∈R恒成立，求实数k的范围；
    （3）对于定义在[p，q]上的函数m（x），设x0=p，xn=q，用任意xi（i=1，2，…，n-1）将[p，q]划分成n个小区间，其中xi-1＜xi＜xi+1，若存在一个常数M＞0，使得不等式|m（x0）-m（x1）|+|m（x1）-m（x2）|+…+|m（xn-1）-m（xn）|≤M恒成立，则称函数m（x）为在[p，q]上的有界变差函数，试证明函数f（x）是在[1，3]上的有界变差函数，并求出M的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图所示，沿河有A、B两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污
    水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为f（m）=25•m0.7（万元），m表示污水流量，铺设管道的费用（包括管道费）$g（x）=3.2\sqrt{x}$（万元），x表示输送污水管道的长度（千米）；
    已知城镇A和城镇B的污水流量分别为m1=3、m2=5，A、B两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）
    （1）若在城镇A和城镇B单独建厂，共需多少总费用？
    （2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为x千米，求联合建厂的总费用y与x的函数关系
    式，并求y的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若矩阵$（\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}）$满足：a11，a12，a21，a22∈{0，1}，且$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|$=0，则这样的互不相等的矩阵共有（　　）
    A．2个B．6个C．8个D．10个

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．不等式$\frac{（x+4）（x+3）}{{{x^2}-5x+4}}＜0$的解集为（-4，-3）∪（1，4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．（1）3${\;}^{1+lo{g}_{3}2}$=6． 
    （2）${log_3}\frac{1}{2}+{log_3}\frac{2}{3}+{log_3}\frac{3}{4}+…+{log_3}\frac{80}{81}$=-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知△ABC中，三条边a，b，c所对的角分别为A、B、C，且a2+b2-c2=ab
    （Ⅰ）求角C的大小；
    （Ⅱ）若f（x）=$\sqrt{3}$sinxcosx+cos2x，求f（B）的最大值，并判断此时△ABC$；\\;的$的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．数列{an}的通项公式为an=$\frac{1}{{n}^{2}+2n}$，其前n项和为Sn，则S10的值为（　　）
    A．1-$\frac{1}{12}$B．$\frac{1}{2}$（1-$\frac{1}{12}$）C．$\frac{1}{2}$（$\frac{3}{2}$-$\frac{1}{12}$）D．$\frac{1}{2}$（$\frac{3}{2}$-$\frac{1}{11}$-$\frac{1}{12}$）

    查看答案和解析>>

    同步练习册答案