如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.
现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50m/min.在甲出发2min后，乙从A乘缆车到B，在B处停留1min后，再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min，山路AC长为1260m，经测量，cosA＝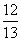
，cosC＝
.
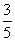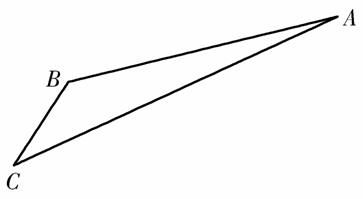
(1)求索道AB的长；
(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？
(1)在△ABC中，因为cosA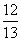＝，cosC＝，
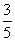所以sinA＝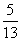
，sinC＝
.
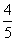从而sinB＝sin[π－(A＋C)]
＝sin(A＋C)
＝sinAcosC＋cosAsinC
＝×＋×＝
.
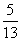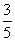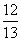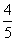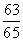由正弦定理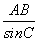
＝
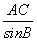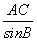，得AB＝×sinC＝
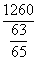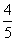×＝1040(m)．
所以索道AB的长为1040m.
(2)假设乙出发tmin后，甲、乙两游客距离为d，此时，甲行走了(100＋50t)m，乙距离A处130tm，
所以由余弦定理得d2＝(100＋50t)2＋(130t)2－2×130t×(100＋50t)×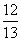＝200(37t2－70t＋50)，
因0≤t≤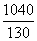
，即0≤t≤8，故当t＝
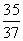(min)时，甲、乙两游客距离最短．
科目：高中数学 来源： 题型：
在△ABC中，角A，B，C的对边分别为a，b，c. 已知A＝
，bsin(＋C)－csin(＋B)＝a.
(1)求证：B－C＝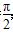
；
(2)若a＝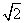
，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知A船在灯塔C北偏东80°处，且A到C距离为2km，B船在灯塔C北偏西40°，AB两船距离为3km，则B到C的距离为( )
A.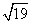
km B．(
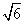－1)km
C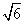．(＋1)km D.
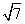km
查看答案和解析>>
科目：高中数学 来源： 题型：
某校运动会开幕式上举行升旗仪式，旗杆正好处在坡度15°的看台的某一列的正前方，从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10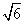m(如图所示)，旗杆底部与第一排在一个水平面上．若国歌长度约为50s，升旗手应以多少m/s的速度匀速升旗？
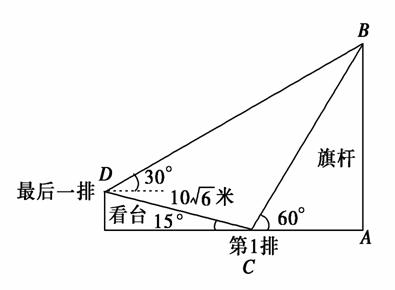
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，α∈
，则cos(α＋
)＝( )
B．－
＝
，则B的值为( )
则目标函数z＝3x－2y的最小值为( )