
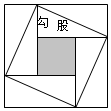
 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”.如图是该弦图变化得到,它是用八个全等的直角三角形拼接而成.若图中勾、股分别为2,5,一粒豆子随机投入大正方形中,则落到阴影部分(含边界)概率是$\frac{9}{49}$.
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”.如图是该弦图变化得到,它是用八个全等的直角三角形拼接而成.若图中勾、股分别为2,5,一粒豆子随机投入大正方形中,则落到阴影部分(含边界)概率是$\frac{9}{49}$.  怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3,4} | B. | {0,1,2} | C. | {0,2,4} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{16}$ | B. | $\frac{5}{4}$ | C. | -$\frac{15}{16}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com