练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
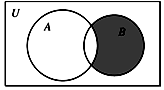
    15．设全集U=N*，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（　　）
    A．{2}B．{4，6}C．{1，3，5}D．{2，4，6}

    分析 由韦恩图可知阴影部分表示的集合为（CUA）∩B，根据集合的运算求解即可．

    解答 解：由韦恩图可知阴影部分表示的集合为（CUA）∩B，
    ∴（CUA）∩B={4，6}．
    故选B

    点评 本小题主要考查Venn图表达集合的关系及运算、Venn图的应用等基础知识，考查数形结合思想．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知过抛物线G：y2=2px（p＞0）焦点F的直线l与抛物线G交于M、N两点（M在x轴上方），满足$\overrightarrow{MF}=3\overrightarrow{FN}$，$|{MN}|=\frac{16}{3}$，则以M为圆心且与抛物线准线相切的圆的标准方程为（　　）
    A．${（{x-\frac{1}{3}}）^2}+{（{y-\frac{{2\sqrt{3}}}{3}}）^2}=\frac{16}{3}$B．${（{x-\frac{1}{3}}）^2}+{（{y-\frac{{\sqrt{3}}}{3}}）^2}=\frac{16}{3}$
    C．${（{x-3}）^2}+{（{y-2\sqrt{3}}）^2}=16$D．${（{x-3}）^2}+{（{y-\sqrt{3}}）^2}=16$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．过点M（2，-2p）引抛物线x2=2py（p＞0）的切线，切点分别为A，B，若$|{AB}|=4\sqrt{10}$，则p的值是（　　）
    A．1或2B．$\sqrt{2}$或2C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若圆锥曲线Γ：$\frac{x^2}{m}+\frac{y^2}{5}$=1（m≠0且m≠5）的一个焦点与抛物线y2=8x的焦点重合，则实数m=（　　）
    A．9B．7C．1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知M是抛物线C：y2=2px（p＞0）上一点，F是抛物线C的焦点，若|MF|=p，K是抛物线C的准线与x轴的交点，则∠MKF=（　　）
    A．45°B．30°C．15°D．60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．一袋中有7个大小相同的小球，其中有2个红球，3个黄球，2个蓝球，从中任取3个小球．
    （I）求红、黄、蓝三种颜色的小球各取1个的概率；
    （II）设X表示取到的蓝色小球的个数，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若正项等比数列{an}，已知a1=4且a52=16a2•a6，则$\frac{1}{\sqrt{{a}_{1}}}$+$\frac{2}{\sqrt{{a}_{2}}}$+$\frac{3}{\sqrt{{a}_{3}}}$+…+$\frac{n}{\sqrt{{a}_{n}}}$=2-$\frac{n+2}{{2}^{n}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知各项不为零的数列{an}的前n项的和为Sn，且满足Sn=λan-1，若{an}为递增数列，则λ的取值范围为λ＜0或λ＞1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．祖冲之之子祖暅是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等．此即祖暅原理．利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为h（0＜h＜2）的平面截该几何体，则截面面积为（　　）
    A．4πB．πh2C．π（2-h）2D．π（4-h2）

    查看答案和解析>>

    同步练习册答案