
| A. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{2\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | B. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | ||
| C. | ${({x-3})^2}+{({y-2\sqrt{3}})^2}=16$ | D. | ${({x-3})^2}+{({y-\sqrt{3}})^2}=16$ |
分析 求出直线l的斜率,可得直线方程,与抛物线方程联立,利用|MN|,求出p,可得M的坐标,即可求出以M为圆心且与抛物线准线相切的圆的标准方程.
解答 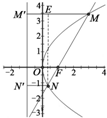 解:如图,过点N作NE⊥MM′,由抛物线的定义,|MM′|=|MF|,|NN′|=|NF|.
解:如图,过点N作NE⊥MM′,由抛物线的定义,|MM′|=|MF|,|NN′|=|NF|.
解三角形EMN,得∠EMF=$\frac{π}{3}$,所以直线l的斜率为$\sqrt{3}$,
其方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),
与抛物线方程联立可得3x2-5px+$\frac{3}{4}$p2=0,
∴x1+x2=$\frac{5}{3}$p,
∴|MN|=$\frac{8}{3}$p=$\frac{16}{3}$,
∴p=2,
∴M(3,2$\sqrt{3}$),r=4,
∴圆的标准方程为(x-3)2+(y-2$\sqrt{3}$)2=16.
故选:C.
点评 本题主要考查抛物线定义以及抛物线的性质,以M为圆心且与抛物线准线相切的圆的标准方程的求法,考查转化思想以及数形结合思想的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①③ | C. | ①② | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6种 | B. | 24种 | C. | 30种 | D. | 36种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
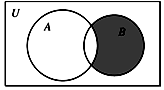 设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {2,4,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com