
分析 (1)由已知数列的前n项和求得an=Sn-Sn-1=2n+k-1(n≥2),再求得首项,验证首项成立可得数列通项公式,结合a1,a4,a13成等比数列求得k,则通项公式可求;
(2)把(1)中求得的通项公式代入${b_n}=\frac{4}{{({a_n}+1)({a_{n+1}}+3)}}$,整理后利用裂项相消法求得数列{bn}的前n项和为Tn,放缩可得${T_n}<\frac{5}{12}$.
解答 (1)解:由${S_n}={n^2}+kn$,有
an=Sn-Sn-1=2n+k-1(n≥2),
又a1=S1=k+1,
∴an=2n+k-1.
∵a1,a4,a13成等比数列,∴${{a}_{4}}^{2}={a}_{1}{a}_{13}$,
即(2×4+k-1)2=(2×1+k-1)(2×13+k-1),解得k=2.
∴an=2n-1;
(2)证明:∵${b_n}=\frac{4}{{({a_n}+1)({a_{n+1}}+3)}}$=$\frac{4}{(2n+2)(2n+6)}=\frac{1}{(n+1)(n+3)}$.
∴${b}_{n}=\frac{1}{2}(\frac{1}{n+1}-\frac{1}{n+3})$.
∴Tn=b1+b2+…+bn=$\frac{1}{2}[(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})+(\frac{1}{4}-\frac{1}{6})+…+$$(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})+(\frac{1}{n+1}-\frac{1}{n+3})]$
=$\frac{1}{2}(\frac{1}{2}+\frac{1}{3}-\frac{1}{n+2}-\frac{1}{n+3})$=$\frac{5}{12}-\frac{1}{2}(\frac{1}{n+2}+\frac{1}{n+3})$$<\frac{5}{12}$.
点评 本题考查数列递推式,考查了由数列的前n项和求数列的通项公式,训练了裂项相消法求数列的前n项和,属中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
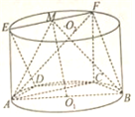 在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.
在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{π}{45}$ | D. | $\frac{45-π}{45}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{2\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | B. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | ||
| C. | ${({x-3})^2}+{({y-2\sqrt{3}})^2}=16$ | D. | ${({x-3})^2}+{({y-\sqrt{3}})^2}=16$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | $\sqrt{2}$或2 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com