练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    二次函数f(x)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

    (1)求f(x)的解析式．

    (2)在区间[－1,1]上，y＝f(x)的图象恒在y＝2x＋m的图象上方，试确定实数m的范围．


    解　(1)设f(x)＝ax2＋bx＋c(a≠0)，由f(0)＝1，得c＝1，故f(x)＝ax2＋bx＋1.

    因为f(x＋1)－f(x)＝2x，

    所以a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x.

    即2ax＋a＋b＝2x，所以

    所以f(x)＝x2－x＋1.

    (2)由题意得x2－x＋1>2x＋m在[－1,1]上恒成立，

    即x2－3x＋1－m>0在[－1,1]上恒成立．

    设g(x)＝x2－3x＋1－m，其图象的对称轴为直线x＝，所以g(x)在[－1,1]上递减．

    故只需g(1)>0，即12－3×1＋1－m>0，解得m<－1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数f(x)＝则f＝(　　)

    A．9                                    B.

    C．－9                                  D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    ．已知函数f(x)＝e|x－a|(a为常数)，若f(x)在区间[1，＋∞)上是增函数，则a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上是单调增函数．如果实数t满足f(lnt)＋f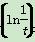<2f(1)时，那么t的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    关于x的二次方程(m＋3)x2－4mx＋2m－1＝0的两根异号，且负根的绝对值比正根大，那么实数m的取值范围是(　　)

    A．－3<m<0                              B．0<m<3

    C．m<－3或m>0                          D．m<0或m>3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax2－2x＋1.

    (1)试讨论函数f(x)的单调性．

    (2)若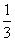≤a≤1，且f(x)在[1,3]上的最大值为M(a)，最小值为N(a)，令g(a)＝M(a)－N(a)，求g(a)的表达式．

    (3)在(2)的条件下，求证：g(a)≥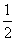

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝则方程f(x)＝的解集为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的奇函数f(x)，当x∈(0，＋∞)时，f(x)＝log2x，则不等式f(x)<－1的解集是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为L1＝5.06x－0.15x2和L2＝2x，其中x为销售量(单位：辆)．若该公司在这两地共销售15辆车，则能获得的最大利润为(　　)

    A．45.606万元                           B．45.6万元

    C．45.56万元                            D．45.51万元

    查看答案和解析>>

    同步练习册答案