
分析 利用向量的数量积,求出f(θ),将其转换成含有t的一元二次函数,讨论对称轴的取值,判断其最大值.
解答 解:f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$+2=sin2θ+2m(cosθ-1)+2=-cos2θ+2mcosθ-2m+3,
令cosθ=t,t∈[-1,1]
f(t)=-t2+2mt-2m+3,t∈[-1,1]
对称轴t=m,
当m<1,f(t)[-1,1]单调递减,当t=-1取最大值为-4m+3<0,
∴m>$\frac{3}{4}$,
此时m∈($\frac{3}{4}$,1),
当m≥1,f(t)[-1,1]单调递增,当t=1时取最大值2,不满足,
当0<m<1时,当x=m取最大值,最大值为-(m+1)2+4>0,
m>1或m<-3,不满足,
综上可知,m∈($\frac{3}{4}$,1)时,对任意θ∈R,f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$+2<0成立.
点评 本题考查向量的数量积及一元二次函数对称轴的取值判断函数的最值,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | -2+2i | B. | -2+4i | C. | -1+i | D. | -1+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
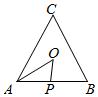 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )| A. | 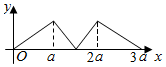 | B. | 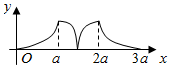 | ||
| C. | 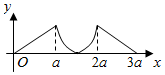 | D. | 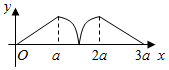 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com