
分析 (1)先求出对立事件的概率,在得出选手甲至少得3分的概率;
(2)分别求出在A,B区的得分的数学期望,从而得出不等式,解出p的范围.
解答 解:(1)选手甲在A区设计不得分的概率为(1-$\frac{1}{3}$)3=$\frac{8}{27}$,
∴选手甲在A区设计至少得3分的概率为1-$\frac{8}{27}$=$\frac{19}{27}$.
(2)设选手甲在A区的得分为X,在乙区的得分为Y,
则X的可能取值为0,3,6,9,Y的可能取值为0,2,4,
则P(X=0)=$\frac{8}{27}$,P(X=3)=${C}_{3}^{1}•$$\frac{1}{3}$•($\frac{2}{3}$)2=$\frac{4}{9}$,P(X=6)=${C}_{3}^{2}•$($\frac{1}{3}$)2•$\frac{2}{3}$=$\frac{2}{9}$,P(X=9)=($\frac{1}{3}$)3=$\frac{1}{27}$,
P(Y=0)=(1-p)2,P(Y=2)=${C}_{2}^{1}$•p(1-p),P(Y=4)=p2,
∴E(X)=0×$\frac{8}{27}$+3×$\frac{4}{9}$+6×$\frac{2}{9}$+9×$\frac{1}{27}$=3,
E(Y)=0×(1-p)2+2×2p(1-p)+4p2=4p,
∴3<4p,又0<p<1,
∴$\frac{3}{4}<P<1$.
点评 本题考查了相互独立事件的概率计算,离散型随机变量的数学期望,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
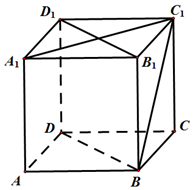 如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;
如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b⇒ac2>bc2 | B. | a<b<0⇒a2b>b3 | ||
| C. | $\frac{a}{b}$>1⇒a>b且b>0 | D. | a3>b3,ab>0⇒$\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=$\sqrt{3}$
如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com