练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，直线y=x与椭圆C交于点E，F，直线y=-x与椭圆C交于点G，H，且四边形EHFG的面积为$\frac{16}{5}$．
    （1）求椭圆C的方程；
    （2）过椭圆C的左顶点A作直线l1交椭圆C于另一点P，过点A作垂直于l1的直线l1，l2交椭圆C于另一点Q，当直线l1的斜率变化时，直线PQ是否过x轴上的一定点？若过定点，求出该定点的坐标，若不过定点，请说明理由．

    分析 （1）利用椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，得出a=2b，直线y=x代入椭圆C，可得$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1，x=$\frac{2\sqrt{5}}{5}$b，利用四边形EHFG的面积为$\frac{16}{5}$，求出b，可得a，即可求得椭圆的方程；
    （2）设直线l1的方程代入椭圆的方程，消去y，整理得一元二次方程，由韦达定理，可求得P的坐标，以-$\frac{1}{k}$代入，可得Q（$\frac{2{k}^{2}-8}{{k}^{2}+4}$，-$\frac{4k}{{k}^{2}+4}$），从而可求PQ的直线方程，令y=0，即可得到结论．

    解答 解：（1）∵椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，
    ∴$\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$，
    ∴a=2b，
    直线y=x代入椭圆C，可得$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1，∴x=$\frac{2\sqrt{5}}{5}$b，
    ∵直线y=x与椭圆C交于点E，F，直线y=-x与椭圆C交于点G，H，且四边形EHFG的面积为$\frac{16}{5}$，
    ∴（$\frac{4\sqrt{5}}{5}$b）2=$\frac{16}{5}$，
    ∴b=1，
    ∴a=2，
    ∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1；
    （2）设P（x1，y1），Q（x2，y2），直线斜率为k，则直线l1的方程为y=k（x+2）
    把它代入椭圆的方程，消去y，整理得：（1+4k2）x2+16k2x+（16k2-4）=0
    由韦达定理得-2+x1=-$\frac{16{k}^{2}}{1+4{k}^{2}}$，
    ∴x1=$\frac{2-8{k}^{2}}{1+4{k}^{2}}$，
    ∴y1=k（x1+2）=$\frac{4k}{1+4{k}^{2}}$，∴P（$\frac{2-8{k}^{2}}{1+4{k}^{2}}$，$\frac{4k}{1+4{k}^{2}}$），
    以-$\frac{1}{k}$代入，可得Q（$\frac{2{k}^{2}-8}{{k}^{2}+4}$，-$\frac{4k}{{k}^{2}+4}$），则kPQ=-$\frac{5k}{4（{k}^{2}-1）}$
    ∴PQ的直线方程为y-$\frac{4k}{1+4{k}^{2}}$=-$\frac{5k}{4（{k}^{2}-1）}$（x-$\frac{2-8{k}^{2}}{1+4{k}^{2}}$），
    令y=0，则x=$\frac{16k（{k}^{2}-1）}{5k（1+4{k}^{2}）}$+$\frac{2-8{k}^{2}}{1+4{k}^{2}}$=-$\frac{6}{5}$．
    ∴直线PQ过x轴上的一定点（-$\frac{6}{5}$，0）．

    点评 本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，综合性强．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．已知θ是第一象限的角，若sin4θ+cos4θ=$\frac{5}{9}$，则sin2θ等于（　　）
    A．$\frac{4}{3}$B．$-\frac{2}{3}$C．$\frac{{2\sqrt{2}}}{3}$D．$-\frac{{2\sqrt{2}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．Sn为等差数列{an}的前n项和，且a1=1，S7=28，记bn=[lgan]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg99]=1．
    （Ⅰ）求b1，b11，b101；
    （Ⅱ）求数列{bn}的前1000项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．椭圆$\frac{x^2}{4}$+y2=1的焦距为2$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．将函数f（x）=cos（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}}$）图象上每一点的横坐标伸长为原来的2倍（纵坐标不变），再向右平移$\frac{π}{6}$个单位长度得到y=cosx的图象，则函数f（x）的单调递增区间为（　　）
    A．[kπ-$\frac{2π}{3}$，kπ+$\frac{π}{3}}$]（k∈Z）B．[kπ-$\frac{7π}{12}$，kπ-$\frac{π}{12}}$]（k∈Z）
    C．[4kπ-$\frac{7π}{3}$，kπ-$\frac{π}{3}}$]（k∈Z）D．[4kπ-$\frac{π}{3}$，kπ+$\frac{5π}{3}}$]（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．下列调查：
    ①每隔5年进行人口普查；
    ②报社进行舆论调查；
    ③灯泡使用寿命的调查；
    ④对入学报名者的学历检查；
    ⑤从20台电视机中抽出3台进行质量检查，
    其中适合用抽样调查的是（　　）
    A．①②③B．②③⑤C．②③④D．①③⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知点M（1，0），A，B是椭圆$\frac{{x}^{2}}{4}$+y2=1上的动点，且$\overrightarrow{MA}•\overrightarrow{MB}$=0，则$\overrightarrow{MA}•\overrightarrow{BA}$的取值范围是[$\frac{2}{3}$，9]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数y=Asin（ωx+φ）的部分图象如图所示，则（　　）
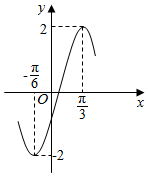
    A．y=2sin（2x-$\frac{π}{6}$）B．y=2sin（2x-$\frac{π}{3}$）C．y=2sin（x+$\frac{π}{6}$）D．y=2sin（x+$\frac{π}{3}$）

    查看答案和解析>>

    同步练习册答案