练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知动点A在椭圆 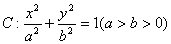上，动点B在直线 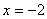上，且满足 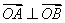（O为坐标原点），椭圆C上点 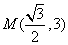到两焦点距离之和为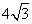

      (I)求椭圆C方程。(Ⅱ)判断直线AB与圆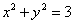的位置关系，并证明你的结论。



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设函数f（x）＝lnx，h（x）＝f（x）＋．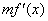

    （1）求函数h（x）的单调区间；

    （2）当m＝e（e为自然对数的底数）时，若h（n）－h（x）＜对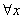＞0恒成立，求实数n的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数，若方程恰有四个不相等的实数根，则实数的取值范围是____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A，B，若圆 上存在点P．使得 ，

    则正数的取值范围为

    A.[4，6]      B.[5，6]          C. [4，5]         D.[3，6]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列 满足 ，则 _______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则下列不等式①, ②,③, ④

    中，正确的有(      )  

    A.1个                B.2个            C.3个           D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


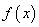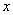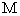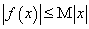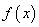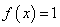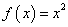    如果函数对任意的实数，存在常数，使得不等式恒成立，那么就称函数为有界泛函．给出下面三个函数：①；②；③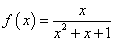．其中属于有界泛函的是（      ）

    A．①③                 B．②             C．③           D．①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    抛物线上到焦点的距离等于10的点的坐标为

    A．(-8,  8)                                               B．(8,  8)

    C．(-8,  -8) 或(8,  -8)                               D． (-8,  8) 或(8,  8)  

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某学校组织学生进行社会主义核心价值观的知识竞赛，进入决赛的共有20名学生，他们的决赛成绩如下表所示：

    决赛成绩/分

    95

    90

    85

    80

    人数

    4

    6

    8

    2

    那么20名学生决赛成绩的众数和中位数分别是（   ）．

    A．85, 90                   B．85, 87.5            C．90, 85           D．95, 90

    查看答案和解析>>

    同步练习册答案