
分析 (1)根据绝对值的性质,分类讨论,即可求出不等式的解集,
(2)根据柯西不等式即可求出答案.
解答 解:(1)①当$x<-\frac{1}{2}$时,不等式等价为$-(x-\frac{1}{2})-(x+\frac{1}{2})≤3$,即-2x≤3,$x≥-\frac{3}{2}$,此时$-\frac{3}{2}≤x<-\frac{1}{2}$;
②当$-\frac{1}{2}≤x≤\frac{1}{2}$时,不等式等价为$(x-\frac{1}{2})-(x+\frac{1}{2})≤3$,即-1≤3,恒成立,此时$-\frac{1}{2}≤x≤\frac{1}{2}$;
③当$x>\frac{1}{2}$时,不等式等价为$(x-\frac{1}{2})+(x+\frac{1}{2})≤3$,即2x≤3,$x≤\frac{3}{2}$,此时$\frac{1}{2}<x≤\frac{3}{2}$,
综上不等式的解为$-\frac{3}{2}≤x≤\frac{3}{2}$,所以不等式的解集为$A=\{x\left|{-\frac{3}{2}≤x≤\frac{3}{2}}\right.\}$.
(2)函数的定义域为[1,5],且y>0,y=5×$\sqrt{x-1}$+$\sqrt{2}$×$\sqrt{5-x}$≤$\sqrt{{5}^{2}+(\sqrt{2})^{2}}$×$\sqrt{(\sqrt{x-1})^{2}+(\sqrt{5-x})^{2}}$=$\sqrt{27×4}$=6$\sqrt{3}$,
当且仅当$\sqrt{2}×\sqrt{x-1}=5×\sqrt{5-x}$时,等号成立,即$x=\frac{127}{27}$时,函数取最大值$6\sqrt{3}$
点评 本题考查了绝对值不等式的解法和柯西不等式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
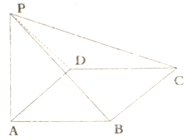 四棱锥P-ABCD的底面是菱形,∠BAD=60°,PA⊥底面ABCD,PA=AB=a,E为棱PC上点.
四棱锥P-ABCD的底面是菱形,∠BAD=60°,PA⊥底面ABCD,PA=AB=a,E为棱PC上点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{27}$ | B. | $\frac{27}{19}$ | C. | $\frac{11}{15}$ | D. | $\frac{15}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com