
| A. | 4 | B. | 8 | C. | 11 | D. | 13 |
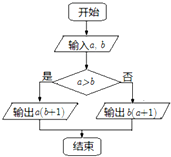
分析 模拟程序框图的运行过程,得出该程序框图运行的结果是计算并输出M=a?b=$\left\{\begin{array}{l}{a(b+1)}&{a>b}\\{b(a+1)}&{a≤b}\end{array}\right.$的值,利用特殊角的三角函数值计算比较,即可求值得解.
解答 解:模拟程序框图的运行过程,得出该程序框图运行的结果是计算并输出M=a?b=$\left\{\begin{array}{l}{a(b+1)}&{a>b}\\{b(a+1)}&{a≤b}\end{array}\right.$,
∵2tan$\frac{π}{4}$=2>sin$\frac{π}{2}$=1,4cos$\frac{π}{3}$=2<($\frac{1}{3}$)-1=3,
∴$(2tan\frac{π}{4})?sin\frac{π}{2}+(4cos\frac{π}{3})?{(\frac{1}{3})^{-1}}$
=2?1+2?3
=2×(1+1)+3×(2+1)=13.
故选:D.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,从而得出该程序框图运行的结果是什么,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∪B=∅ | C. | A?B | D. | (∁UA)∩B={2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a∈R,f(x)是偶函数 | B. | ?a∈R,f(x)是奇函数 | ||
| C. | ?a∈(0,+∞),f(x)在(-∞,0)上是增函数 | D. | ?a∈(0,+∞),f(x)在(0,+∞)上是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com