
分析 画出函数y=f(x)的图象,通过函数图象可以直观的看出何时取到最值,对称轴以及周期性等问题.
解答 解:画出函数y=f(x)的图象如图所示;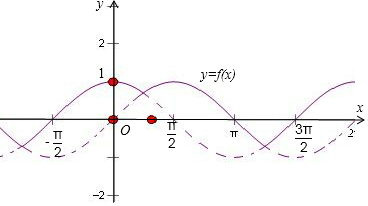
由图可知:
①函数f(x)的值域为[-$\frac{\sqrt{2}}{2}$,1],∴①正确;
②函数f(x)是最小正周期为2π的函数,∴②正确;
③函数f(x)的对称轴为x=kπ+$\frac{π}{4}(k∈{Z})$,∴③正确;
④x=2kπ或x=2kπ+$\frac{π}{2}$(k∈Z)时,函数f(x)取得最大值1,∴④错误;
⑤当且仅当2kπ+π<x<2kπ+$\frac{3}{2}π(k∈{Z})$时,f(x)<0,∴⑤错误;
综上,正确的命题序号是①②③.
故答案为:①②③.
点评 本题考查了分段函数的定义、图象与性质的应用问题,也考查了画图与识图的能力,是中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x0) | B. | -f′(x0) | C. | f′(-x0) | D. | 不一定存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | 5 | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com