练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知正数a，b，c满足4a-2b+25c=0，则lga+lgc-2lgb的最大值为-2．

    分析 将4a-2b+25c=0变形为：4a+25c=2b，利用基本不等式可得：2b$≥2\sqrt{100ac}$；lga+lgc-2lgb=$lg\frac{ac}{{b}^{2}}$，即可求解．

    解答 解：由题意：4a-2b+25c=0，变形为：4a+25c=2b，
    ∵4a+25c$≥2\sqrt{100ac}$，当且仅当4a=25c时，取等号．
    ∴2b$≥2\sqrt{100ac}$；即b2≥100ac
    那么：lga+lgc-2lgb=lg$\frac{ac}{{b}^{2}}$≤lg$\frac{ac}{100ac}$=lg10-2=-2
    故答案为：-2．

    点评 本题考查了对数的运算和基本不等式的运用能力．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知曲线y=1+lnx与过原点的直线相切，则直线的斜率为（　　）
    A．eB．-eC．1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．棱长均为1的正三棱柱ABC-A1B1C1的外接球表面积为$\frac{7π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知集合A={x|x2-16＜0}，B={x|x2-4x+3＞0}，求A∪B，A∩（∁RB）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．与400°终边相同的最小正角是40°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

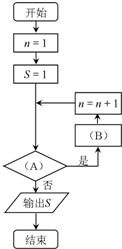    10．已知数列{an}，a1=1，an+1=an+n，计算数列{an}的第20项．现已给出该问题算法的程序框图（如图所示）．为使之能完成上述的算法功能，则在如图判断框中（A）处和（B）处依次应填上合适的语句是（　　）
    A．n≤20，S=S-nB．n≤20，S=S+nC．n≤19，S=S-nD．n≤19，S=S+n

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种，现在餐厅准备了5种不同的荤菜，若要保证每位顾客有210种以上（含210种）的不同选择，则餐厅至少还需准备7种不同的素菜．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知有向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1且$\overrightarrow{a}$，$\overrightarrow{b}$夹角为120°，若$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{d}$=3$\overrightarrow{b}$-$\overrightarrow{a}$，求$\overrightarrow{c}$，$\overrightarrow{d}$两向量夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．圆C：（x-1）2+（y-2）2=25，直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）．
    （1）证明：不论m取什么数，直线l与圆C恒交于两点；
    （2）求直线l被圆C截得的线段的最短长度，并求此时m的值．

    查看答案和解析>>

    同步练习册答案