
| 1 |
| an |
| 1 |
| 4 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 1 |
| a6 |
| ||||
| 6-1 |
| 3 |
| 4 |
| 4 |
| 3n-2 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 1 |
| a6 |
| ||||
| 6-1 |
| 3 |
| 4 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3n-2 |
| 4 |
| 4 |
| 3n-2 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
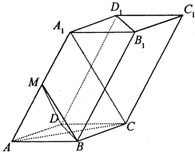 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+2 |
| an+1+2 |
| an+1+2 |
| an+2 |
| 1 |
| 2 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
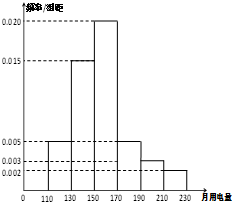 2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
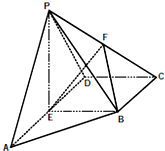 如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=
如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com